董少南1,高 烈2,孫立海3,張敢生4,張寶忠5
（1.本溪市安達爆破工程有限公司，遼寧 本溪 117000；2.本鋼集團公司，遼寧 本溪 117000，3遼寧隆燁爆破工程有限公司，遼寧 本溪 117000，4.遼寧科技學院，遼寧 本溪 117000，5.本鋼礦山實業有限公司，遼寧 本溪 117000）
摘 要：闡述了最優化巖石爆破的理論和方法。提出了爆區的巖石最佳破碎原理、最優炸藥單耗原理、能量平衡分配原理、可碎能帶分布原理、單孔爆破最佳破碎原理和面能比中值化原理。并依據這些原理提出了如下爆破設計方法：按最優炸藥單耗原理計算藥量、按能量均勻度最大化原則布置炮孔、按綜合能量梯度最大化原則安排起爆順序、按可碎能帶分布原理和單孔爆破最佳破碎原理設計裝藥結構及填塞方法。從而實現綜合爆破危害效應最小、綜合爆破效果最佳的目標。
關鍵詞：最優化；巖石爆破；爆炸能量；爆能體
0 引 言
在巖石爆破中，炸藥在巖體中爆炸所釋放的能量，以爆炸應力波和爆轟氣體膨脹壓力的方式傳遞給巖石，使巖石產生破碎，但是真正用于破碎巖石的能量只占炸藥釋放能量的很少部分，大部分都消耗在產生爆破飛石、爆破震動、空氣沖擊波和噪音等有害效應方面。因此如何提高炸藥的能量利用率，最大限度地改善巖石爆破效果具有非常重要的意義。
一般來講，在實際工程爆破中綜合考慮各種因素使總的爆破危害效應最小、總的爆破效果最佳的巖石爆破占絕大多數，因此是我們研究的重點內容。由于這類爆破是以綜合爆破危害效應最小、綜合爆破效果最佳為目標，因此我們把它稱之為最優化巖石爆破。
1 最優化巖石爆破理論的基本內容
要想實現最優化巖石爆破[1]，必須解決以下三個方面的理論問題：一是如何布孔和起爆才能使整個爆區的巖石處于最佳破碎狀態；二是如何選取炸藥單耗才能使整個爆區的炸藥能量利用率處于最佳狀態；三是如何設計裝藥結構與填塞方式才能使每個炮孔的巖石破碎塊度實現最優及炸藥能量利用率達到最高。為了解決這三個問題我們提出了最優化巖石爆破理論，這個理論主要包括爆區的巖石最佳破碎原理、最優炸藥單耗原理、能量平衡分配原理、可碎能帶分布原理、單藥包爆破巖石最佳破碎原理和面能比中值化原理。下面我分別對這幾個基本原理的內容、提出的原因和依據、能夠解決的問題進行闡述。
1.1 爆區的巖石最佳破碎原理
1.1.1 提出的原因和依據
（1）提出的原因
為了解決如何布孔和起爆才能使整個爆區的巖石處于最佳破碎狀態問題，我們提出了爆區的巖石最佳破碎原理[2,3]。雖然在現有理論中也有一些關于布孔和起爆方面的理論，但是這些理論在客觀上還解決不了這個問題。
（2）提出的依據
依據就是存在很多無法用現有理論給予合理解釋的爆破現象，我們認為在這些現象背后一定隱藏著一個影響巖石爆破效果好壞的最本質規律，這個規律就是爆區的最佳破碎原理。
1.1.2 內容
根據爆破實踐和道學原理，我們認為整個爆區的巖石最佳破碎原理是：在炸藥和巖石一定的條件下，以綜合效果為最優的巖石爆破中，爆區的巖石破碎效果與整個爆區的炸藥能量分配均勻度、爆破過程中相鄰炮孔巖石的綜合能量梯度成正相關。因此每個爆區要想實現最優化爆破必須使炸藥能量分配均勻度和爆破過程中相鄰炮孔的巖石綜合能量梯度值均達到最大化。這個原理就是整個爆區的巖石最佳破碎原理。要想實現最優化巖石爆破必須符合這個原理。
1.1.3 能量分配均勻度的概念
能量分配均勻度是指爆炸能量在整個爆區巖體中分布的均勻程度。
（1）爆能體與標準爆能體的概念
爆能體：是爆炸能量在巖體中各個方向傳播的能量波波陣面所構成的空間結構體。
標準爆能體：是在標準布孔方式下，兩個相鄰且同時起爆的藥包相切時的爆能體。
（2）爆炸能量分配均勻度的計算：
爆炸能量分布均勻度計算有絕對均勻度和相對均勻度的區別。計算方法和所起作用也略有不同。一個爆區孔眼布置的好壞，要綜合考慮這兩個參數。
（3）絕對均勻度的計算
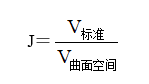
(1)
式中，J為爆炸能量分布的絕對均勻度；V標準為爆區內所有藥包的標準爆能體所占據的空間體積；V曲面空間為爆區內與最外側標準爆能體相切的曲面空間所圍成的空間體積。
（4）相對均勻度的計算
相對均勻度的計算方法是：首先把爆區分解成若干個基本單元，針對每個基本單元計算它在標準藥包布置方式下的絕對均勻度，并定為基準1；然后把實際布孔的絕對均勻度與標準布孔方式的絕對均勻度相比，所得比值就是此基本單元的相對均勻度。
1.1.4 能量梯度的定義及計算
所謂能量梯度就是指爆炸能量密度在單位距離上的變化量。
（1）能量梯度的計算
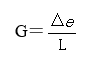
(2)
式中，G為能量梯度；△e為兩相鄰炮孔在同一瞬間能量密度的差值，根據能量密度變化曲線方程進行計算；L為炮孔間距。
1.1.5 爆炸能量密度的變化曲線
從微觀上看每個藥包的爆破過程都是一個由壓應力為主向拉應力為主的轉換過程。在這個過程中如果我們規定壓應力為主的能量密度為正，拉應力為主的能量密度為負[4]。那么從宏觀上看壓應力為主的表現為向外膨脹，拉應力為主的表現為向內收縮。這樣向外膨脹的能量狀態就為正，向內收縮的能量狀態就為負。因此爆破過程就可以看成是一個能量密度高低振蕩的過程。這個過程可以用能量密度變化曲線方程表示，經驗公式如下
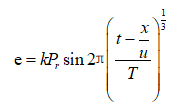
(3)
式中，e為能量密度；u為爆炸能量綜合效應的傳播速度；Pr為巖石中沖擊波峰值壓力；T為巖石破碎時間。
1.1.6 應用與解決的問題
爆區的巖石最佳破碎原理可以解決布孔和起爆的最優化問題。
（1）最佳布孔問題：
根據爆區的巖石最佳破碎原理，得出整個爆區的最佳布孔原則是能量分配均勻度趨向最大化。具體講就是各炮孔的標準爆能體相切時達到最大化。
（2）最佳起爆問題：
根據爆區的巖石最佳破碎原理，得出爆區的最佳起爆原則是相鄰炮孔的巖石綜合能量梯度趨向最大化。具體來講就是計算所有相鄰炮孔在爆破時間內綜合能量梯度最大值時的合理微差間隔時間與合理微差間隔距離，并據此確定合理的起爆網路。
1.2 最優炸藥單耗原理
1.2.1 提出原因
當前最優炸藥量的計算主要是根據利文斯頓最優爆破漏斗理論進行計算，但是這個計算結果與實際用量存在較大差距，因此在工程實際中根據利文斯頓最優爆破漏斗理論計算的值僅僅作為參考，更多的還是根據經驗公式進行計算。所以為了解決最優炸藥量的計算問題，我們提出了最優炸藥單耗原理[5]。
1.2.2 內容
從實踐中我們知道，炸藥單耗過高則爆炸能量轉變為飛石和空氣沖擊波的比例增加，而炸藥單耗過低則爆炸能量轉變為爆破震動的比例增加，只有炸藥單耗在一個合適值時爆炸能量用于破碎的能量最高（即有用能量利用率最高），那么炸藥單耗取何值時炸藥的有用能量利用率最高呢？通過研究我們認為當爆破作用指數n＝0.5時炸藥的有用能量利用率最高。關于這個結論可以從理論和實踐兩個方面得到證明。
1.2.3 理論證明
對于單個球形藥包來說，我們把整個爆炸能量分成水平能量和垂直能量兩部分，每部分再分成有用能量和無用能量兩部分，我們再求當兩部分有用能量乘積取最大值時的爆破作用指數n值，則結論即可得到證明。
設兩部分有用能量的乘積為y，整個有用能量為1，水平方向有用能量為E∥有用，垂直方向有用能量E⊥有用。則列方程如下：
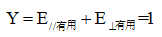
(4)
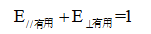
(5)
解得E∥有用＝E⊥有用＝1/2，對于單個球形藥包的爆破漏斗來說，最小抵抗線W是垂直方向有用能量的量度，而爆破漏斗直徑2r是水平方向有用能量的量度，二者相等既是爆破作用指數n＝0.5。因此當爆破作用指數n＝0.5時炸藥的有用能量利用率達到最高。
1.2.4 藥量計算
根據現有理論的體積公式
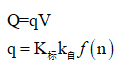
(6)
1.2.5 實踐驗證
依據上面的計算公式，我們可以根據各種巖石標準拋擲爆破的炸藥單耗計算得到各種巖石松動爆破的炸藥單耗。計算所得藥量在實踐中均能得到很好的松動爆破效果。
例如石灰石和鐵礦石最優炸藥單耗計算，按n＝0.5得到它的計算公式為q=0.475K標，對于石灰石K標＝1.0～1.2 kg／m3，鐵礦石K標＝1.8～2.2 kg／m3，則其松動爆破時的最優炸藥單耗值為：石灰石q=0.45～0.6 kg／m3，鐵礦石q=0.85～1.05 kg／m3。而此值與實際需求相符。
1.3 能量平衡分配原理
1.3.1 提出的原因和依據
原因：是為了解決在爆破作用時間內爆破漏斗區域內爆炸能量的計算問題。
依據：就是存在很多爆破現象，表明爆炸能量在巖石中的分配與巖石在各個方向的阻力存在一定規律。這個規律就是能量平衡分配原理。
1.3.2 能量平衡分配原理的內容
所謂能量平衡分配原理就是在通過以爆源為原點的任何直線上，在爆破作用時間內分配的爆炸能量與此傳播方向所受到的阻力乘積的矢量和總是為零。通過這個原理可以計算爆破漏斗范圍內在爆破作用時間內所儲存的爆炸能量和自由面系數的計算問題。
關于能量平衡分配原理可以從動量守恒定律得以證明。證明過程如下：
首先把整個爆炸能量E看作是由各個方向的能量單元e組成。每個能量單元e再分解成每個瞬間dt的能量de組成。由于每個de在以爆源為中心的一條直線上的能量分配與兩個小球在以爆源為中心的直線上碰撞現象物理等效，因此爆炸能量在巖石中的傳輸問題可以看作是一種特殊形式的質點碰撞現象來加以解決。設e1為直線正向分配的能量，e2為直線負向分配的能量，e＝e1＋e2。則
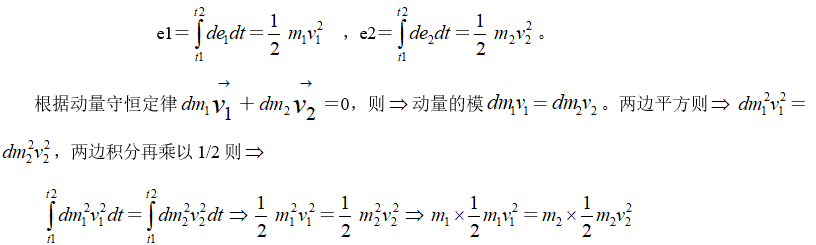
其中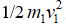
是在直線正向分配的爆炸能量e1，1/2
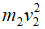是在直線負向分配的爆炸能量e2，
是爆炸能量在正向所掃過的巖石質量，它與爆炸能量在正向傳輸過程中所受到的阻力大小成正比，
是爆炸能量在負向所掃過的巖石質量，它與爆炸能量在負向傳輸過程中所受到的阻力大小成正比。乘以單位矢量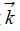
和－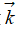
，所以在直線兩個方向上的阻力分別為
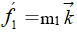和
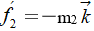。從而證得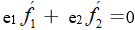
。
1.4 可碎能帶分布原理
1.4.1 提出的原因和依據
原因：根據能量平衡分配原理，我們知道在爆破漏斗區域內有多少爆炸能量儲存。那么這些能量又是如何分配的呢？因為這個問題不解決，我們就不知道何種分配狀態有利于巖石破碎、何種分配狀態不利于巖石破碎，因而也就不知道應當如何調整裝藥結構。所以為了解決這個問題我們提出了可碎能帶分布原理。
依據：就是存在很多爆破現象，表明從爆源到自由面之間爆炸能量是分級分布的，其能量密度分布在數值上是不連續的；在空間上每級都是呈一定分布寬度的能帶，而每條能帶又都具有近似相同的能量密度，能帶的能量密度從爆源到自由面依次呈等比級數降低。
1.4.2 可碎能帶分布原理的內容
（1）可碎能帶的形成：
炸藥爆炸產生的能量以能量脈沖的形式在巖石中向外傳播，由于能量脈沖在壓實后的巖石中傳播速度加快及遇到高能量密度區傳播受阻將形成反射，因此就在巖石中形成一條條不同能量密度的能帶在向外傳播，在沒有自由面的無限介質巖石中，裂隙區和彈性振動區處的能帶能量密度分布在數值上呈連續性變化。相鄰巖石質點之間僅有較小的變形，因此形成不了巖石破碎。而在有自由面的有限介質巖石中，由于能帶在向外傳播過程中遇到自由面傳播受阻，因而就從自由面開始形成能量集聚，集聚的能量反射產生能量疊加形成更高密度能帶。當其能量密度達到有自由面的巖石破碎強度時就形成第一條具備破碎條件的能帶，我們稱之為可碎能帶。從爆源來的后續能量遇到第一條可碎能帶后又將發生反射形成第二條可碎能帶。這樣就從自由面開始到爆源之間依次形成若干條可碎能帶。這些可碎能帶的能量密度分布在數值上呈間斷性跳躍變化，這種間斷性跳躍分布特性造成相鄰巖石質點之間產生較大的剪切和拉伸變形，從而使巖石產生破碎。因此可碎能帶的產生是巖石破碎的首要條件。
（2）可碎能帶的分布：
空間上：可碎能帶的空間分布狀況可以用能帶級數N、能帶寬度B及能帶的能量密度ei等參數進行描述。
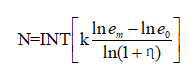
(7)
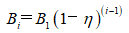
(8)
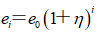
(9)
式中，k為修正系數；B1為第一條可碎能帶寬度；η為相鄰可碎能帶的能量密度變化率，與巖石性質和最小抵抗線W相關；e0為巖石破碎所要求的最低能量密度；em為爆源在巖石中所產生的最高能量密度。
時間上：可碎能帶在時間分布上是瞬時動態變化的。每條能帶都有開始形成時間Tic、存留時間Til、巖石開始破碎時間Tiks和巖石結束破碎時間TiJs。對于單孔爆破來講，可以通過調整這些參數來改善爆破效果，這幾個參數如下：
第一條可碎能帶形成時間T1c，也是第一條能帶巖石開始破碎時間T1ks。T1c＝w/v＋△T1；
第一條可碎能帶巖石結束破碎時間T1Js＝T1c＋△T1s；
最后一條可碎能帶形成時間Tnc＝2w/v＋△Tn；
最后一條可碎能帶開始消失時間Tnkx＝Tnc＋Tnl。此后可碎能帶體系被破壞，如果此時爆破漏斗內巖石還未開始破碎，那么能量就以震動形式傳走，不會形成巖石破碎。所以根據這幾個參數關系可以推導出單孔爆破巖石最佳破碎原理。
1.4.3 單孔爆破巖石最佳破碎原理的內容
在單孔爆破[6,7]中，可碎能帶的形成是巖石破碎的基礎，巖石爆破效果的好壞與可碎能帶的能量密度和時空參數密切相關，在實際爆破工作中主要通過調整第一條可碎能帶巖石開始破碎時間T1ks、第一條可碎能帶巖石結束破碎時間T1Js和最后一條可碎能帶開始消失時間Tnkx來改善爆破效果。一般來講有下列三種情況：
（1）當T1ks≥Tnkx時：爆破漏斗內巖石不能很好破碎，不能形成完整的可碎能帶體系，因此也就不能形成爆破漏斗。
（2）當T1Js＜Tnkx時：爆破漏斗內巖石將產生過粉碎，過多能量將以爆破飛石動能、空氣沖擊波和噪音的形式傳走。
（3）T1ks＜Tnkx≤T1Js時：能夠形成完整的可碎能帶體系，爆破漏斗內巖石能夠得到很好的破碎，并形成完整的爆破漏斗，且當T1ks＜Tnkx＝T1Js爆破漏斗內巖石實現最佳破碎。
1.5 面能比中值化原理
1.5.1 提出的原因和依據
原因：在巖石爆破中，巖石為什么這樣破碎而不那樣破碎，是什么因素在控制巖石的破碎形狀和數量，為了解決這個問題我們提出了面能比中值化原理。
依據：依據之一就是爆破巖塊之間形狀存在相似性的現象。這種現象表明有一種力量在支配巖石的破碎形狀。這種力量就是面能比最小化原理。
依據之二就是在爆破漏斗內巖石是多級多塊度破碎而不是單級單塊度破碎。這種現象表明有一種力量在支配巖石的破碎數量。這種力量就是面能比最大化原理。
1.5.2 面能比中值化原理的內容
面能比中值化原理是由兩個對立統一的原理組成，這兩個原理就是面能比最大化原理和面能比最小化原理（即最小阻力原理）。所謂面能比中值化原理就是在由巖石和炸藥組成的系統中，為了同時滿足這兩個對立統一因素陰陽相搏而取中道的一項破巖原理。因為巖石爆破就是由巖石和炸藥所組成的陰陽對立統一系統，在這個系統中炸藥為陽、巖石為陰。炸藥爆炸能量向外發散，其特性是以最小的代價（即最小的破碎面積）獲得最大的能量釋放，因此爆炸能量總是沿著最小阻力方向開始釋放，即遵循最小阻力原理，從面能比角度看它遵循的是面能比最小化原理。而巖石特性是以最小的代價（即以最小的巖石體積）捕獲更多的爆炸能量（即獲得最大破碎面積），因此它總是希望沿著最復雜的曲面形式進行破碎，從面能比角度看它所遵循的是面能比最大化原理。一般來講，面能比最小化原理對巖塊形狀起主要作用，而面能比最大化原理對巖塊形狀起輔助作用。同時面能比最大化原理對巖塊數量起主要作用，而面能比最小化原理對巖塊數量起輔助作用。
（1）面能比最大化原理：
內容：所謂面能比最大化原理就是在爆破作用時間內，儲存在某一巖石區域內的爆炸能量所造成的破碎面積與此區域內的爆炸能量之比總是趨向最大化。面能比可以按下式計算：
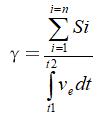
(10)
式中，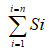
為爆破產生的破碎面面積總和；
為在破碎時間內儲存在該區域巖石中的爆炸能量總和，其值可以根據能量平衡分配原理進行計算。
證明：因為從巖石破碎角度來講，只要某區域內儲存的爆炸能量密度達到巖石破碎所需的最小值，巖石就開始破碎。故有
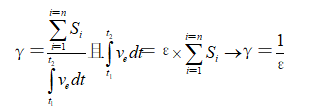
(11)
式中：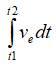
為在爆破時間內儲存在該區域巖石中的爆炸能量總和，其值為定數；ε為巖石單位破碎面積所需的能量，對于特定巖石其值趨向
于單位破碎面積所需的最小值。
因為分子為定數、分母趨向最小值，所以對于特定巖石γ將趨向于最大化。
（2）最小阻力原理（面能比最小化原理）
內容：就是爆炸能量釋放總是最先從最小阻力方向開始。從面能比角度看就是能量釋放總是遵循產生的破碎面與釋放能量之比趨于最小化。
證明：因為從能量釋放角度來講，爆炸能量總會沿著阻力最小路徑釋放，對于各向同性巖石就是沿著最小破碎面積釋放。故有
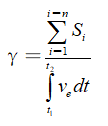
(12)
因為分子趨向最小值、分母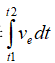
為常量，所以從能量釋放角度看γ又將趨向于最小化。
2 應用技術研究
2.1 爆區設計評價方法
相對爆破效果指數：是用來判斷不同爆破設計方案優劣的指標數。這個指數可以反映出同一爆區的不同爆破設計方案的優劣，指數高的爆破效果就好，指數低的爆破效果就差。它按下列公式計算：
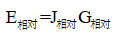
(13)
式中，E相對為相對爆破效果指數；J相對為整個爆破區能量分布的相對均勻度；G相對為整個爆區爆破過程中相鄰炮孔的相對能量梯度。
2.2 裝藥結構設計和填塞方法
2.2.1 “主——輔藥包”法的原理
由于爆破作用指數n＝0.5時的松動爆破可碎能帶時間參數是T1ks＜Tnkx＜T1Js，但不符合單孔爆破最佳破碎T1ks＜Tnkx＝T1Js的條件。因此要想使n＝0.5時的松動爆破符合單孔爆破最佳破碎條件，必須通過增加爆源處可碎能帶的存留時間（即增大Tnkx）或減少自由面處的可碎能帶的結束破碎時間（即減小T1Js）。而增大Tnkx的途徑可以通過增大最小抵抗線W和提高填塞質量獲得。而減小T1Js的途徑可以通過減小最小抵抗線W和改變裝藥結構獲得。在爆破作用指數不變的情況下只能通過提高填塞質量和改變裝藥結構獲得。為此我們提出“主——輔藥包”裝藥爆破法[8]。輔助藥包同時實現以下兩個基本功能。一是起到引導巖石破碎的作用。二是起到提高填塞質量的作用。這就是“主——輔藥包”裝藥爆破法的基本原理。
3 結束語
提出最優化巖石爆破理論的初衷，是為了解決如何進行爆破設計才能實現爆破危害效應最小、爆破有用效應最大的目標。為了實現這個目標，首先研究了應當如何布孔和起爆才能使爆區巖石達到最佳破碎狀態問題，為此提出了爆區巖石最佳破碎原理。其次研究了應當如何計算藥量才能使爆區炸藥能量利用率達到最高問題，為此提出了最優炸藥單耗原理。其三研究了應當如何設置裝藥結構和填塞方式才能使單個炮孔實現最優化爆破問題。
為實現單孔爆破的最優化首先必須解決巖石的破碎機理問題，而這個問題又歸結為解決爆破區域內爆炸能量的計算、分配和釋放形成巖塊問題。為此首先提出能量平衡分配原理以解決爆破區域內爆炸能量的計算問題。進一步又研究爆破區域內爆炸能量的分配問題，提出可碎能帶分布原理和單藥包爆破最佳破碎原理。再進一步為解決如何形成巖塊的形狀和數量問題，又提出面能比中值化原理。
最后，根據上述原理得出實現最優化巖石爆破的最佳途徑是：一、根據爆炸能量分布均勻度最大化原則布置炮孔。二、根據相鄰炮孔的綜合能量梯度最大化原則安排起爆網絡。三、根據主輔藥包法原則設置裝藥結構和填塞。
在長期的爆破實踐中它基本上可以解決此類爆破現場出現的所有問題。客觀地說這種理論更多地是來源于實踐經驗，而缺乏精確實驗數據的支持，因此還有很多地方需要驗證和深入研究。
參考文獻
[1] 姚鵬.炸藥與巖石的匹配分析研究[D].武漢理工大學,2011.
[2] 孔祥松,劉響鐘,周紀軍,等.巖石工程爆破破碎的機理研究[J].礦業研究與開發,2013,33(04):118-121.
[3] 盧海湘,廖明超.巖石爆破破碎機理的試驗探討[J].湖南有色金屬,2001(06):6-8.
[4] 王永青,汪旭光.乳化炸藥能量密度與爆破效果的關系[J].有色金屬,2003(01):102-104.
[5] 劉慧,馮叔瑜.炸藥單耗對爆破塊度分布影響的理論探討[J].爆炸與沖擊,1997(04):72-75.
[6] 林發展,陳培煌,劉四德,等.鉆爆法施工中單孔爆破的精細化數值模擬[J].工程爆破,2017,23(06):11-16.
[7] 李忠武,楊永英.巖石爆破松動破壞作用范圍確定的探討[J].工程爆破,1997(02):4-8.
[8] 劉義恒,劉先魁,林素彬.雙層主、輔條形藥包松動爆破起爆順序的探討[J].工程爆破,1997(03):60-64.